Crop
The Main Idea
Crop circles are fascinating. They get their name from the work of two British painters, Doug Bower and Dave Chorley. In the late 1970’s they had the idea of going out into a field in the middle of the night with a peg, a piece of rope, a couple of big boards on ropes (called “stompers”), and a comfortable amount of beer. They planted the peg in the ground, tied the rope to it, and then walked away from the peg, holding the rope, until it was taut. Keeping the rope taut, they put the stomper on the ground, pushing down the grain, and stepped on it hard (hence the name). Then they took a step forward, keeping the rope taut, and stomped again. When they’d gone all the way around the circle, they shortened the rope a little and repeated. When they were done, they’d flattened a solid circle in the middle of the field. The grain was all lying in the same direction (clockwise or counter-clockwise), which gave the result a nice flowing appearance. The artists then went back home for a good night’s sleep.
These circles caught the eye of the local press, which wrote them up as a local mystery and included photographs. Probably for fun as much as anything, the news stories suggested that they might be the work of space aliens. And thus was born the field of “cereology” (really!), or the discipline of studying what are now more accurately called “crop formations/”
“Doug and Dave” eventually admitted that they were behind the phenomenon, and even gave a demonstration of how they did it for the press, but it was too late. The cereologists were already convinced that space aliens were the true circle makers, and they dismissed the two artists as frauds who were trying to take the credit. Over time, many new midnight artists and the people who study their work have elevated the game. The artists make designs that are ever-richer and more complex and beautiful, and the cereologists invent new devices and theories to study the results and prove that they must be the work of extraterrestrials.
Things got even more exciting when an astronomer named Gerald Hawkins got involved. He noticed that some formations had a lot of geometry behind them (of course), and claimed that they could only have been made by someone with vastly more sophisticated geometric knowledge than any known to man. He even claimed to have developed a set of remarkable geometric theorems that proved his case, though he died before ever telling anyone quite what those theorems were. The story of “Hawkins’ Five Theorems” has grown over time, approaching the level of mythology.
The practice and culture of crop circles is absolutely fascinating. The social aspect of it is especially wild, with the constant back-and-forth of the artists admitting their work, even with videotapes of them making it, countered by the cereologists labeling them “hoaxers” for taking credit for the work actually performed by space aliens using invisible flying craft, Q-rays, and other exotic technologies for bending little stalks of grain.
Today some crop formations are openly made in broad daylight by commercial organizations, largely for advertising purposes. We’ve seen crop formations in the form of company logos and even faces of famous people. Although cereologists freely admit that these are made by people, since the formation process is often a well-attended and well-documented local event, they remain steadfast that the geometric formations that appear in the middle of the night are the ones really worth study, bearing traces of their non-human origins.
I thought it would be fun to come up with a little language that could capture, in just a few lines, the geometry of a crop formation. But even better, I wanted the language to then prepare step-by-step instructions for making that formation using nothing but the circlemaker’s traditional tools: pegs, ropes, and stompers. And those instructions had to be easy and clear enough that you could carry them out in the middle of the night, with little to no moonlight, by only a few people at most. It wouldn’t hurt if they could pull it off while slightly inebriated.
I even fantasized that this could contribute a little to the debate between circlemakers and cereologists. After all, if you could demonstrate that just about any formation, no matter how complex, could be easily constructed with just pegs and ropes, that might take a little bit of the oomph out of the argument for space aliens. I was, of course, completely wrong about that.
My Crop language was designed to capture the kinds of geometric ideas that are frequently embodied in crop formations. The goal was produce expressions that are short and clear. Technically, the language uses a stack-based postfix approach. The language is pretty short: there are only about 25 operators, including all the little stuff. You can do arithmetic on scalars and points, compute some basic geometrical relationships, and execute loops based on regular polygons. The full language description is given in the publications listed at the bottom in the “References” section.
Below are some examples of real formations found in the wild, accompanied by their “blueprint” or geometric skeleton, and the Crop code for that blueprint (in fact, the PostScript for the figures was created by these Crop programs; I just colored them in). Once you stomp out the lines and circles and arcs of the blueprint, you only need to stomp down the crop inside some of their regions to make your formation. I’m listing here only a few examples, but I’ve been able to write nice Crop code for almost every crop formation I’ve seen. The holdouts tend to be those that are either obviously or suspiciously commercial, and probably weren’t make with only the traditional tools of pegs, ropes, and stompers.
These formations are traditionally named for the village or town that is closest to the field. Photographs of these formations are widely available on the web, but I’m not showing them here. My experience is that most cereologists support themselves, at least in part, by copyrighting and then selling their photographs, so it would be wrong to include them here without permission. This adds another interesting layer to the symbiosis between the artists and the cereologists: the artists need the cereologists to document and publicize their work, and the cereologists need the artists to produce that work. In a disappointing asymmetry, though, only the cereologists are making money from this exchange, not the artists who make it.
Folly Barn 2001
We’ll start with the very pretty “Folly Barn 2001” crop formation. The formation itself is shown below on the left, and to its right is its geometric skeleton. As you can see, the formation consists of fifteen circles and a triangle. Excluding the triangle (which isn’t necessary to make the formation), we can represent this formation in Crop with just three lines of code. The first two lines create the twelve circles that make up the crescents. The last line creates the three circles corresponding to the innermost dot, the circle around it, and the large circle surrounding the whole figure.

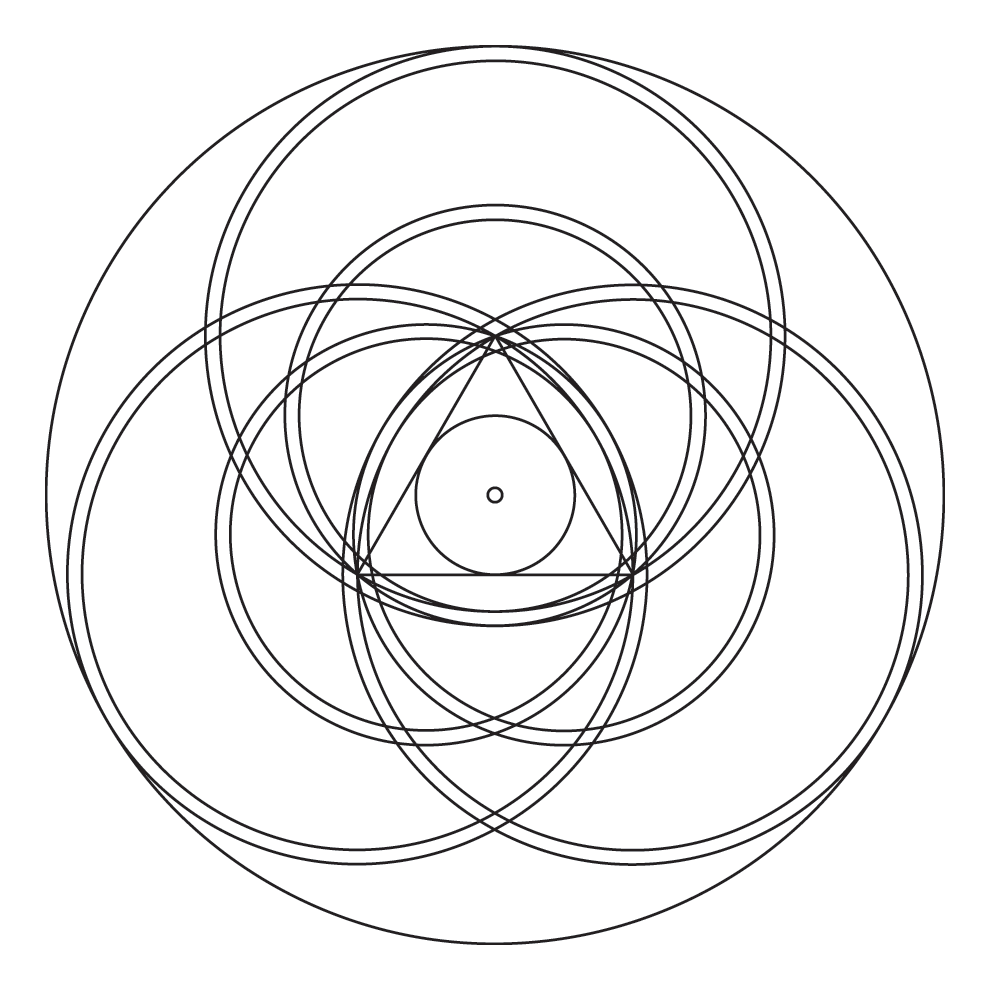
[ V0 < 3.46 3.64 > circle ] # 3 2 0 ngonloop
[ V0 < 2.46 2.64 > circle ] # 3 1 0 ngonloop
# < 1 5.64 0.09 > circle
Tegdown Hill 2003
The “Tegdown Hill 2003” formation is a lovely flower-like design. The first four lines of the Crop code for this geometry merely set variables for the radii of the various circles. The actual geometry requires only two lines of code.

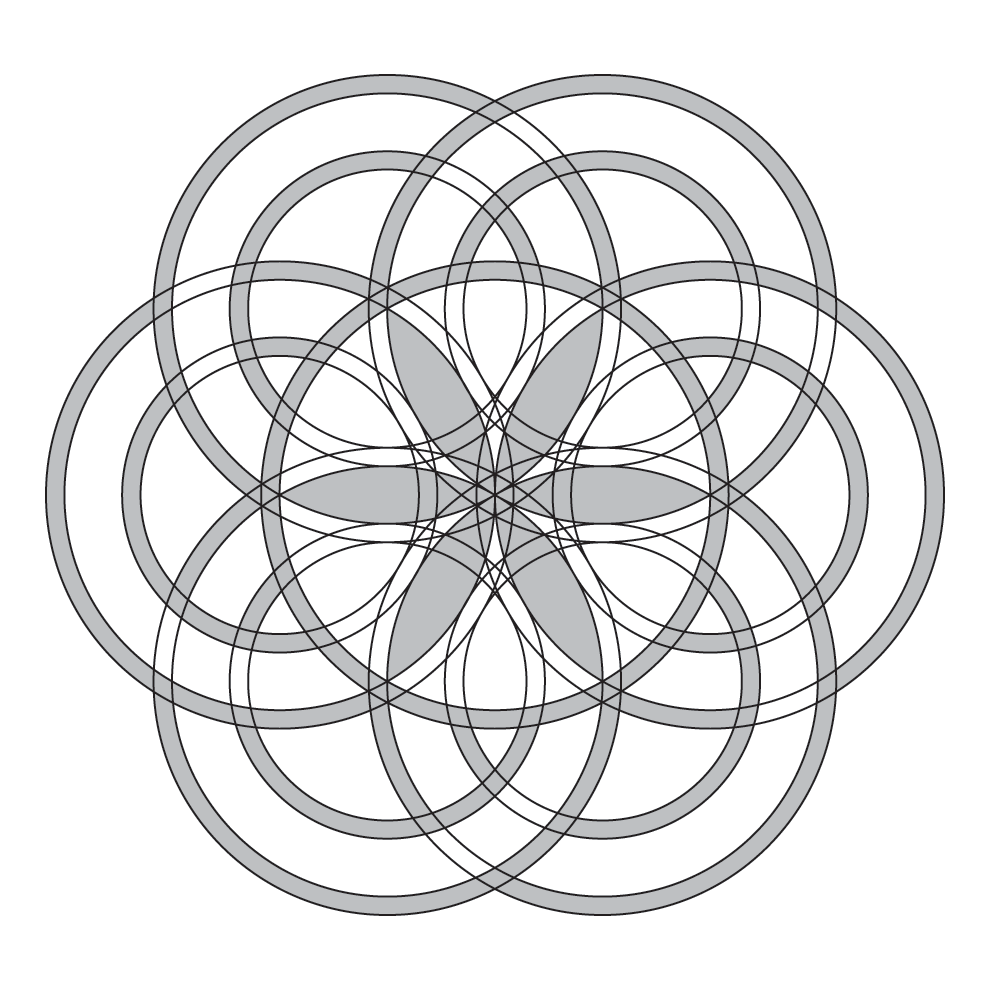
1.0 Ar name
1.08565 Br name
0.732051 Cr name
0.646402 Dr name
[ V0 < Ar Br Cr Dr > circle ] # 6 Ar 0 ngonloop
# < Ar Br > circle
Windmill Hill 2003
The “Windmill Hill 2003” formation is simple, elegant, and beautiful.

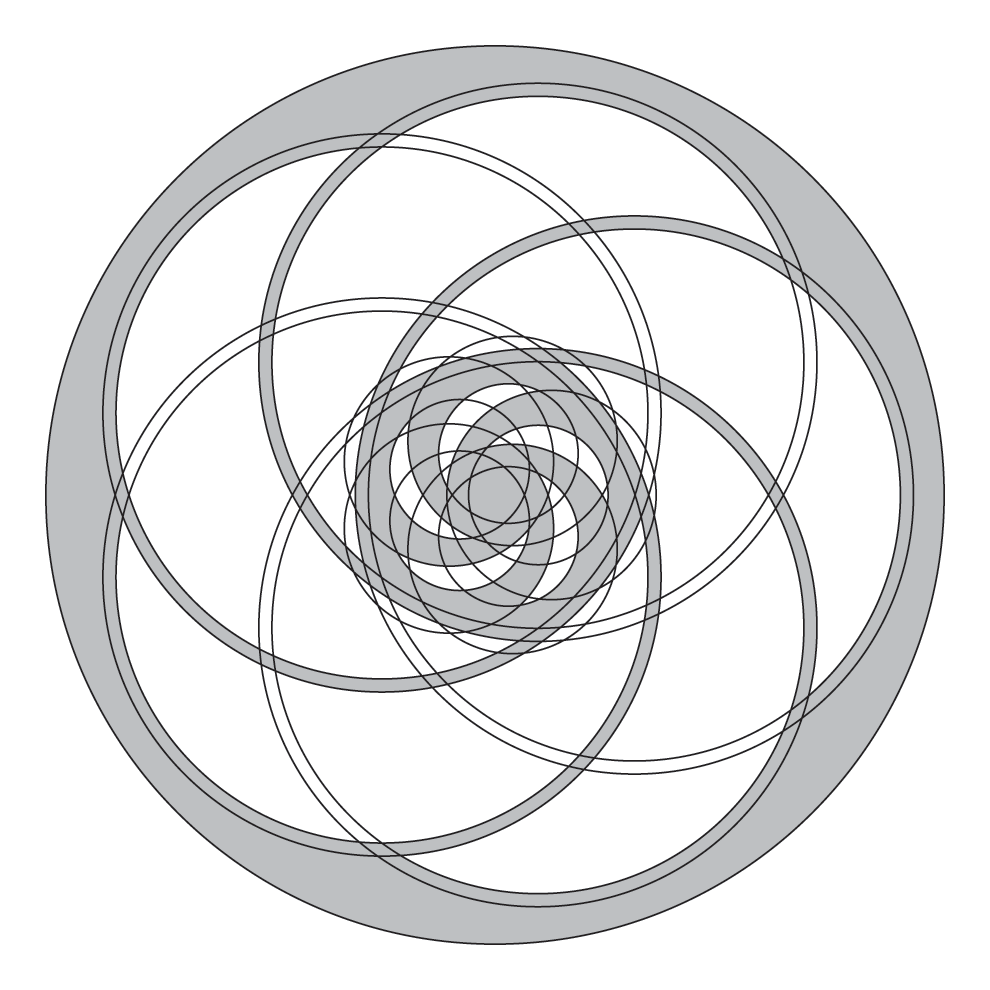
# < 10.3 > circle
[ V0 < 1.6 > circle ] # 5 1 0 ngonloop
[ V0 < 2.4 > circle ] # 5 1.3 0 ngonloop
[ V0 < 6.1 6.4 > circle ] # 5 3.2 0 ngonloop
West Stowell 2003
The “West Stowell 2003” formation has lot of very interesting interaction between the many little geometrical elements. It’s also a great example of mixing straight and circular elements in one design. The first four lines of the Crop code just set variables for the radii of the four circles involved in the design. The second four lines produce all the geometry.

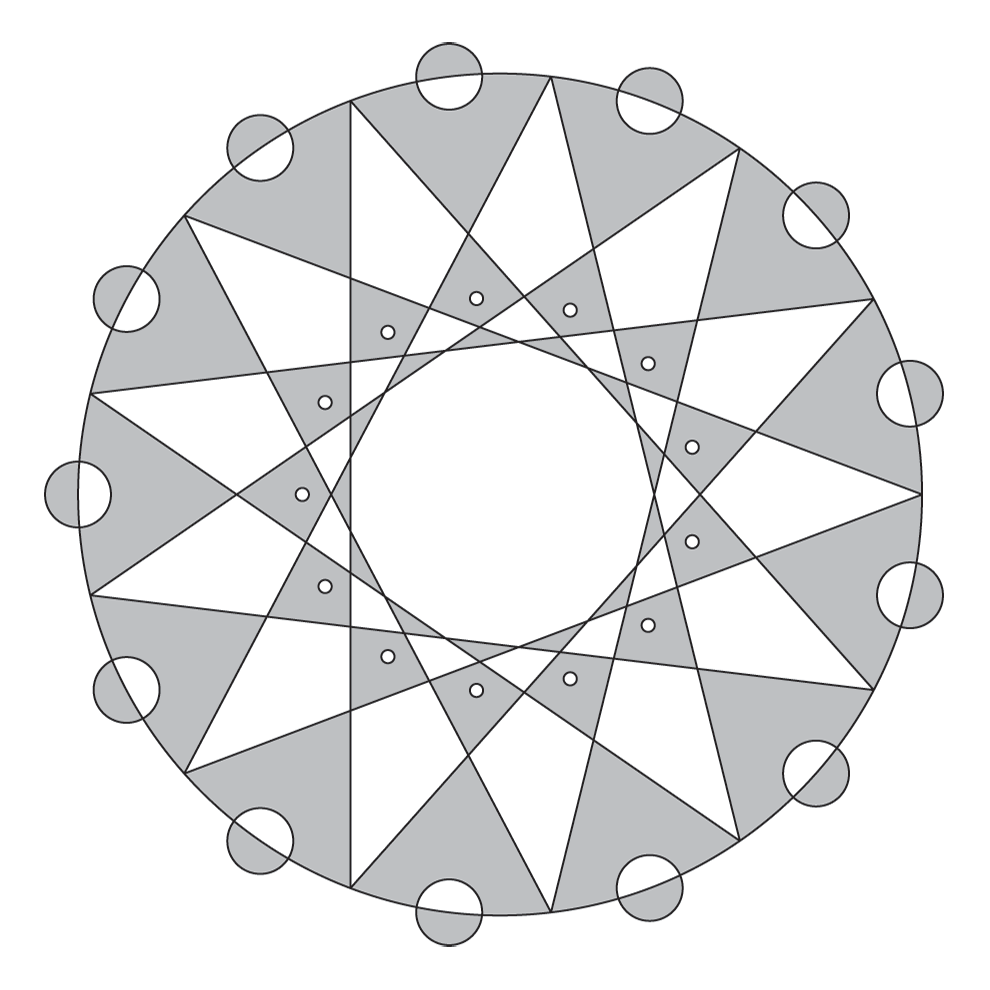
1 Ar name
Ar 5 * 64 / Br name
Ar 30 * 64 / Cr name
Ar 64 / Dr name
# < Ar > circle
[ < V0 V5 > line ] # 13 Ar 0 ngonloop
[ V0 < Br > circle ] # 13 Ar % ngonloop
[ V0 < Dr > circle ] # 13 Cr % ngonloop
Seattle 2004
To prove that my program not only could describe crop formations, but could actually tell you how to make them, I made one of my own. First, I designed a new formation and wrote the Crop code for it. As you can see, I got a bit ambitious, and designed something that required more code than any of the existing formations I’d studied.

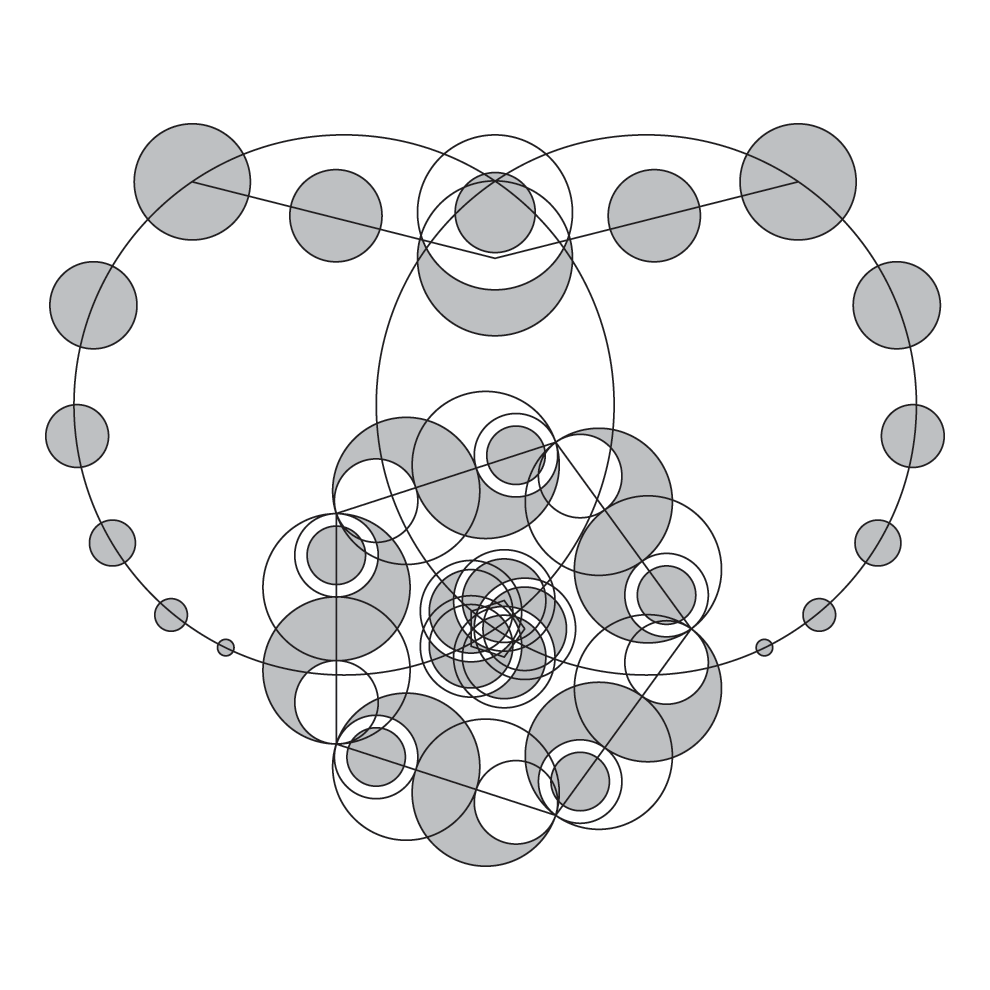
// make central iris
[ V0 < 25.290 30.708 > circle ]
# 5 18 0 ngonloop
// make outer swirls
25.108 d1 name
44.251 d2 name
17.576 d3 name
# 5 118 0 makengon N1 name
[
N1 V0 d1 pwalk < d1 > circle
N1 V0 d2 pwalk < d2 > circle
V0 V1 distance edgelen name
N1 V0 edgelen d1 – pwalk < d1 > circle
N1 V0 edgelen d2 – pwalk < d2 > circle
N1 V0 edgelen d3 – pwalk < d3 > circle
]
# 5 118 0 ngonloop
Then I had my system print out the instructions for making the formation with pegs and ropes. Although I wasn’t able to locate a field where I could get permission to make my formation, a friend of mine offered the surface of a parking lot he helped to maintain. So not too long after, on a winter’s day that started rainy but eventually cleared up, two friends and I went out to make a crop circle!
 To make the crop formation we followed the instructions printed out by my program to the letter. I figured in the middle of the night you wouldn’t really be able to second-guess your instructions, so neither should we. But we did have to make some accommodations due to our changed environment. Since we couldn’t drive a peg into the concrete, one of us would pretend to be the peg and just stood there holding the rope (actually, we used colored string, which was easier to work with). Instead of stomping the skeleton we used chalk to draw our shapes. And instead of stomping the regions that were meant to be filled, we cleaned them off with a pressure washer, revealing the bright concrete under the layers of accumulated dirt.
To make the crop formation we followed the instructions printed out by my program to the letter. I figured in the middle of the night you wouldn’t really be able to second-guess your instructions, so neither should we. But we did have to make some accommodations due to our changed environment. Since we couldn’t drive a peg into the concrete, one of us would pretend to be the peg and just stood there holding the rope (actually, we used colored string, which was easier to work with). Instead of stomping the skeleton we used chalk to draw our shapes. And instead of stomping the regions that were meant to be filled, we cleaned them off with a pressure washer, revealing the bright concrete under the layers of accumulated dirt.
Pressure-washing is slow. Since we wouldn’t have time to make the whole design, we focused on just the central part. As we were finishing up, the sun came out. When we were done, I climbed to the roof of a nearby building and took this photo of my friend Chris waving from our crop formation.

References
Glassner, Andrew S., “Morphs, Mallards, and Montages,” published by AK Peters, Natick, 2004.
Glassner, Andrew S., “Crop Circles, Part 1”, IEEE Computer Graphics & Applications, Volume 24, Number 4, September 2004.
Glassner, Andrew S., “Crop Circles, Part 2”, IEEE Computer Graphics & Applications, Volume 24, Number 5, November 2004.
Leave a Reply
You must be logged in to post a comment.

Leave a Reply
You must be logged in to post a comment.