The Main Idea

Details are important. Every object around us has tons of surface detail: there are the minor scratches, dents, and marks from wear, color imperfections, shiny spots where the paint has worn away or dull spots where the finish is missing, and so on. There’s also detail in the geometry: there’s oranment and decoration in almost every man-made object.

Crafting all this detail for 3D objects can be time-consuming, so over the years people have developed many different kinds of shortcuts. Textures are a key tool for adding both surface and geometric detail. To get even more expressive, methods like shape amplification can take a simple model and add more geometry to it, trying to make the new stuff feel harmonious with what was there before. Some inspiration can also be found in fractals, where we can automatically add more detail that is similar to the base object.

In this project, I also wanted to create rich geometry from a simple object, but I took a different approach. My idea is based on the idea of search and replace. Your favorite text editor probably has such a function, letting you find and replace all instances of, say, “canine” with “dog”. I decided to do the same thing for 3D shapes. The first version of the program kept things simple, letting you search a model for polygons of a certain type and replace them with new geometry, which can be as complicated as you like. The name of the project comes from the utility built into Unix for searching text files. That program is named grep (the odd name comes from the commands you use to search text in the vi editor). So I adopted the name and I call my technique shape grep.

This picture shows the essence of the idea. At the left we have an equilateral triangle. Actually, this is four smaller triangles of equal size, one in each corner and one in the center (you can’t see them because they’re all touching). I told my program to search this pattern for all triangles, and replace each one with a little pattern of four new triangles, giving us the second image. Note that the new triangles aren’t all in the same orientation: they follow the orientation of the triangle they’re replacing. Though we can’t see the orientations of the four triangles at the far left, you can infer them from how these new triangles are laid out. In this case I replaced equilateral triangles with more equilateral triangles, but you can replace your shapes with any number of any shape of polygon. Furthermore, you can tell the system whether to replace all triangles, or only those that have a specific shape. After this step, I ran my search-and-replace program again, replacing each triangle with another little bundle of five triangles. Finally on the right you can see the result after one more step of shape grep. You can control what happens to the colors on every step; in the last step I picked a set of colors inspired by art made by Native Americans in the Southwest US. This design won a prize at the SIGGRAPH ’92 T-shirt competition.

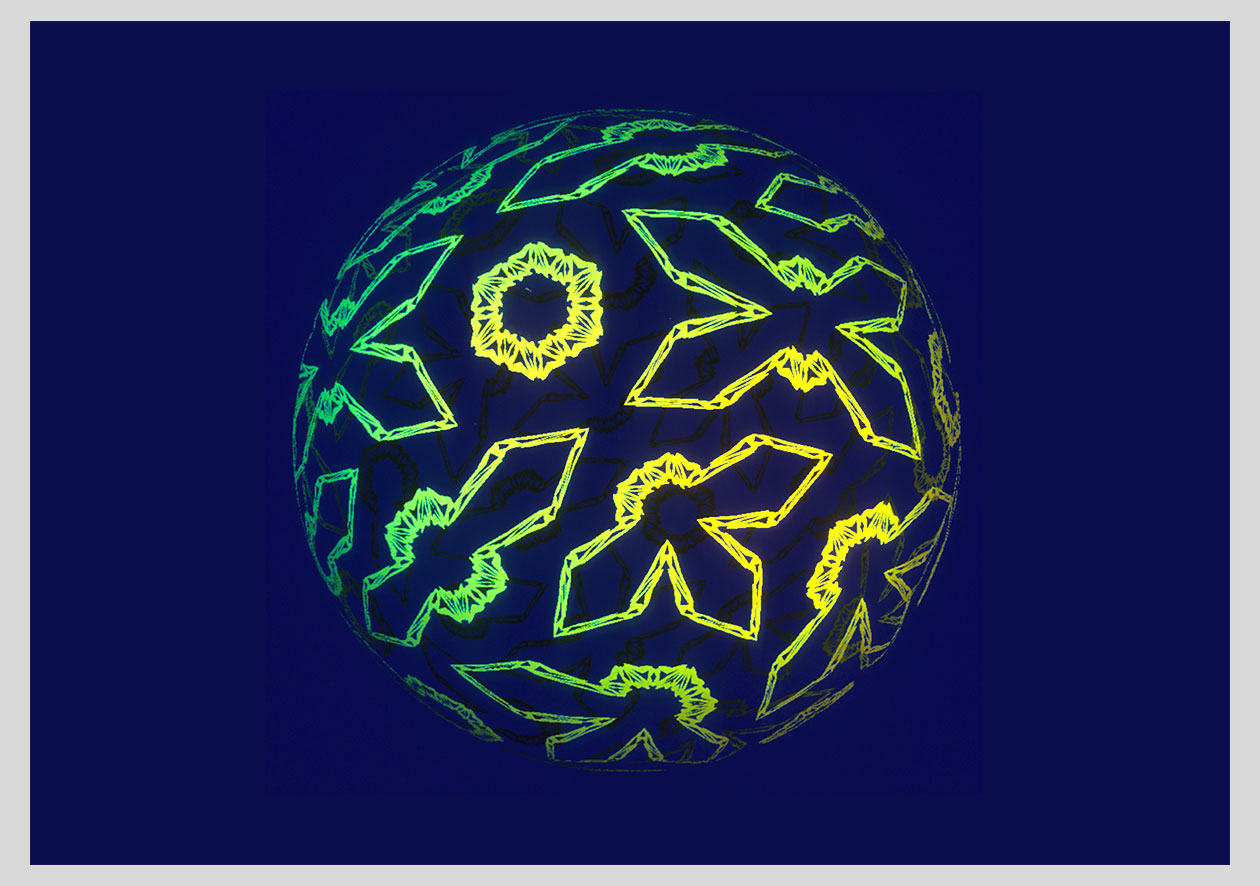
All of the sphere-like images on this page started with an icosahedron. That’s a Platonic solid made of 20 equilateral triangles. The shape has a lot of inherent symmetry, which survives the search-and-replace steps, but that symmetry gets overlaid with new details that add their own feeling. The first version of the program only let you search for individual polygons that had the shape you wanted, but there’s no reason you couldn’t extend this to polyhedra, replacing, say, all the roses in a flower arrangement with daffodils, or all the giant foam fingers at a sports stadium with hand puppets.

I love this kind of process, where you can grow complexity from simplicity. You have a lot of control over what happens here, because you get to design the replacement patterns to get just the kind of effect you’re going for. By applying several repeated passes of shape grep, you can transform a simple shape into something more complicated and interesting. You can imagine animating the transformations over time, creating some wild effects as shapes seem to grow and shed details and patterns over time.

References

Glassner, Andrew S., “A Tutorial on Geometric Replacements”, IEEE Computer Graphics & Applications, volume 12, Number 1, January 1992, pp. 22-36.